Inverse Kinematics
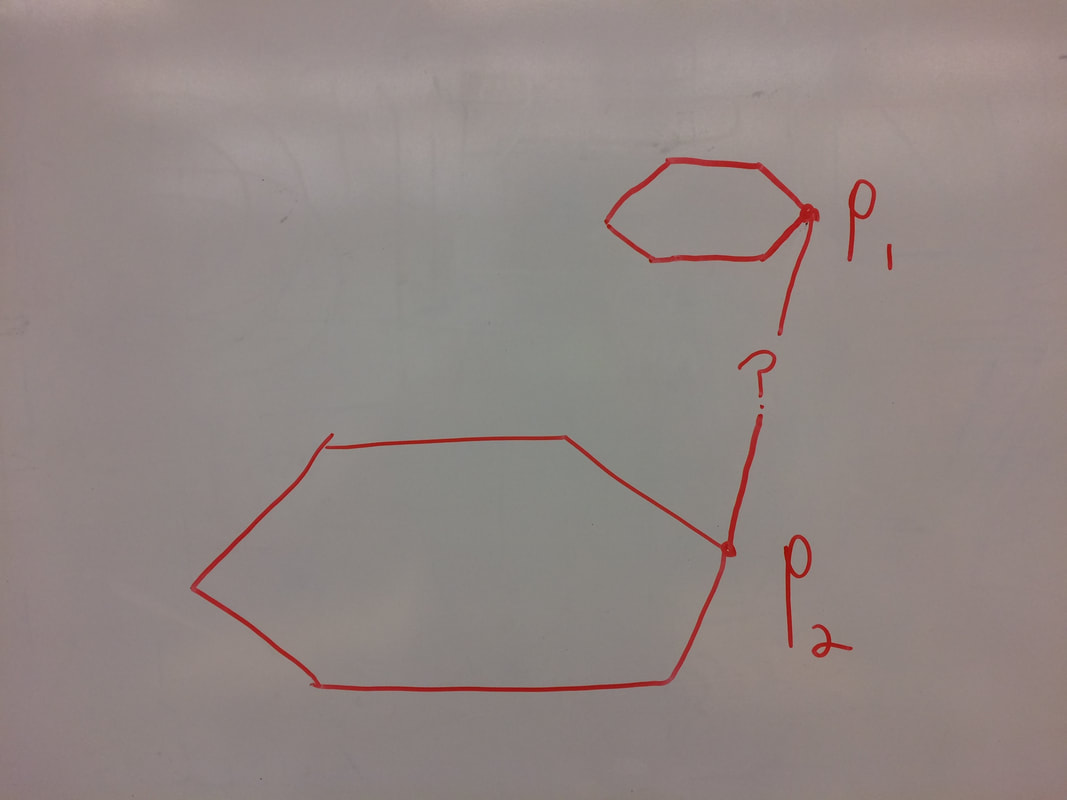
Inverse kinematics are the mathematical operation of calculating ideal servomotor positions to put the platform in a target position and orientation. The inverse kinematics of a Stewart platform are complex, but solvable. First, the upper ball joints' positions are calculated by transforming their original positions by the platform's position and angle. Next, the mathematical models of the servos are placed in some neutral position, and the distance between each lower ball joint and its corresponding upper ball joint is found. These lengths should all be equal to the actual lengths of the diagonal rods, so the servos' angles are optimized using gradient descent until the distances are within an acceptable bound of the actual lengths. Though this method relies on iteration, it is still fast enough to run in real time, since the mathematical operations are all relatively quick. For the inverse kinematics we used code from another POE group. Their github page can be found here.
Forward Kinematics
We used a NN for the Stewart platform's forward kinematics. There is no known computational solution for the forward kinematics, and NNs are the best solution currently available. We tried multiple NNs, and eventually trained a net that was able to calculate the position of the platform within millimetres.
What is a Neural Net?
from Wikipedia, the free encyclopedia
Artificial neural networks (ANNs) or connectionist systems are computing systems inspired by the biological neural networks that constitute animal brains. Such systems learn (progressively improve performance on) tasks by considering examples, generally without task-specific programming.
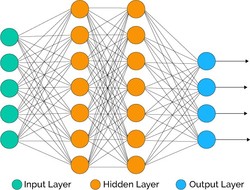
Neural nets work by using layers of interconnected nodes, each of which simulates a neuron. Like neurons, he nodes have two states, active and inactive. The nodes switch on and off based on the previous layer of nodes. They decide whether they are activated or not based on an activation function, which has the states of all the previous nodes as inputs. A the sum the activation function is based on the layer the nodes are in, and a number of coefficients and biases (the nets configuration). The configuration is not specified by the programmer, but are determined during the training of the NN.
The NN is trained by giving it a large number of example problems and solutions (training set). It tests the current configuration of the net, and adjusts it based on the results of the example problems. It repeats this process thousands of times; each time finding a configuration that does better on the training set. Eventually the configuration is saved. The net with that configuration now can take problems like the ones in the training set, and produce outputs very close to the solutions.
from Wikipedia, the free encyclopedia
Artificial neural networks (ANNs) or connectionist systems are computing systems inspired by the biological neural networks that constitute animal brains. Such systems learn (progressively improve performance on) tasks by considering examples, generally without task-specific programming.
Neural nets work by using layers of interconnected nodes, each of which simulates a neuron. Like neurons, he nodes have two states, active and inactive. The nodes switch on and off based on the previous layer of nodes. They decide whether they are activated or not based on an activation function, which has the states of all the previous nodes as inputs. A the sum the activation function is based on the layer the nodes are in, and a number of coefficients and biases (the nets configuration). The configuration is not specified by the programmer, but are determined during the training of the NN.
The NN is trained by giving it a large number of example problems and solutions (training set). It tests the current configuration of the net, and adjusts it based on the results of the example problems. It repeats this process thousands of times; each time finding a configuration that does better on the training set. Eventually the configuration is saved. The net with that configuration now can take problems like the ones in the training set, and produce outputs very close to the solutions.
The NN is trained by giving it a large number of example problems and solutions (training set). It tests the current configuration of the net, and adjusts it based on the results of the example problems. It repeats this process thousands of times; each time finding a configuration that does better on the training set. Eventually the configuration is saved. The net with that configuration now can take problems like the ones in the training set, and produce outputs very close to the solutions. The technical details of the net are below.